ETOOBUSY 🚀 minimal blogging for the impatient
Unbounding the x axis in the rejection method
TL;DR
Where we remove the constraints on the $x$ axis for the rejection method.
In previous post Rejection method we introduced the rejection method generalization with a constraint: our probability density function must be bound to a finite range over the $x$ axis. This is the condition that allows us to use a uniform distribution for selecting a candidate value on the $x$ axis itself, which will be then validated by the random draw over the $y$ axis.
What if we cannot guarantee this constraint, like in the following example?
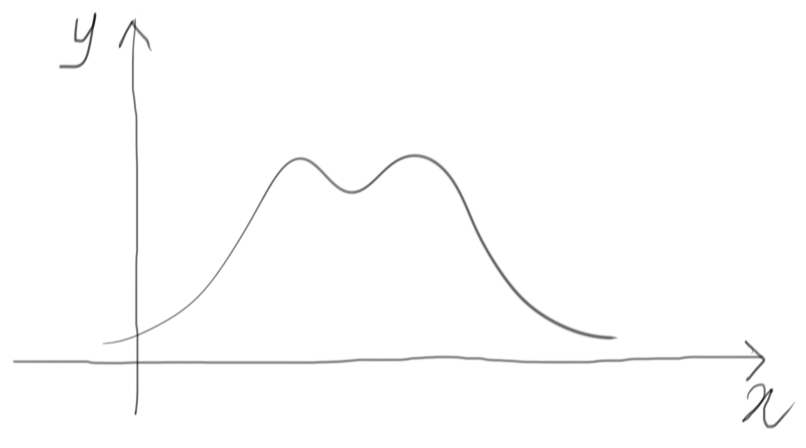
A preliminary observation
The uniform distribution is easy, but not necessarily efficient. We already saw that it can be limiting; moreover, depending on the shape of the target density function, it might also be inefficient.
Nothing binds us to use it, tough. we can just as well use any other density function where we can easily draw values from, and use that instead!
Let’s select something similar, then!
Let’s select a distribution that goes more or less like our target:
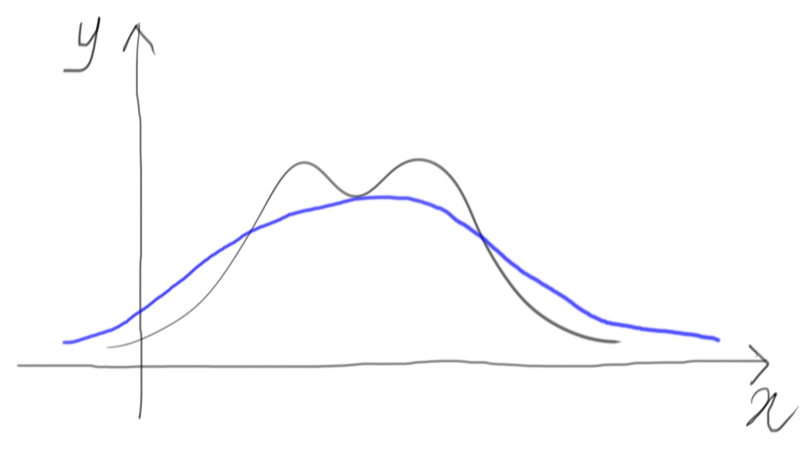
When we generate a sample from this distribution in blue, different small ranges on the $x$ dimensions will have different probabilities to be drawn, according to the shape of this function. This is a selection over the $x$ dimension that guarantees us to overcome the limitation of the uniform function.
What to do on the other dimension?
In the rejection method, after the $x$ dimension we have to draw another value for the $y$ dimension. What is the right segment to consider?
First of all, we rescale the chosen similar density function so that the whole target density remains below, or at most touching:
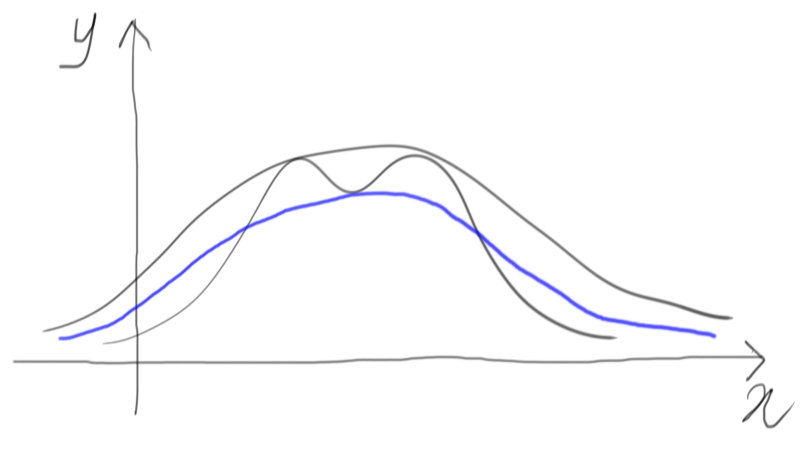
At this point, the vertical segment to consider is from the $x$ axis up to this rescaled function, using a uniform draw over this segment. Whatever comes out below the target function is accepted, whatever goes over is rejected.
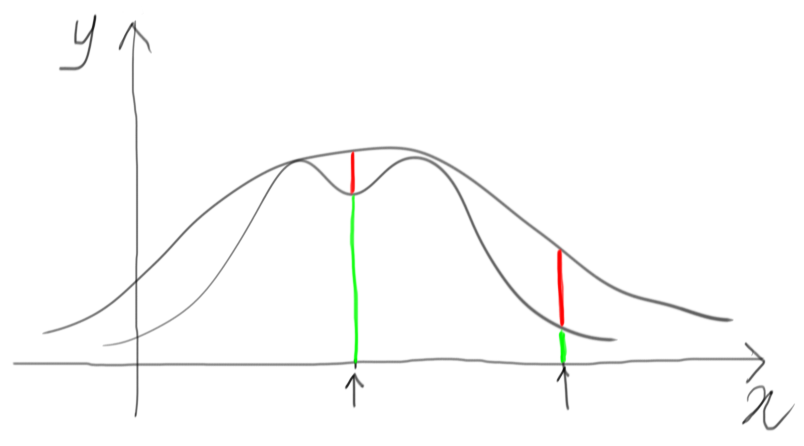
In mathematical terms, if $p(x)$ is our target density function, and $q(x)$ is our choice for a similar function for which we can easily generate samples, we have to find a constant $c$ such that:
\[\forall x: p(x) \leq c \cdot q(x)\]At this point, when we generate a random value $x^*$ using $q(x)$, we will then generate a random value $y^*$ from a uniform distribution between $0$ and $c \cdot q(x^*)$ and apply the following algorithm:
- if $y^* <= p(x^*)$ then the sample is accepted;
- otherwise ($y^* > p(x^*)$), the sample is rejected.
Again, we will not go into a formal demonstration, but it can be easily seen that the combination of the two random draws will always generate points below the scaled density function, and the rejection cuts out the unwanted samples, leaving us with a distribution that matches our expectations.