TL;DR

Let’s take a closer look at the [rejection method][].

In A 4-faces die from a 6-faces die we used the rejection method to generate a D4 die using a D6: just roll it, and remove whatever does not fit your needs.

It turns out that this idea can be generalized to generate more complex samples, based on whatever probability density function.

The following example describes a probability density function, with the non-trivial constraint that its possible values on the $x$ axis are limited between $0$ and $a$:

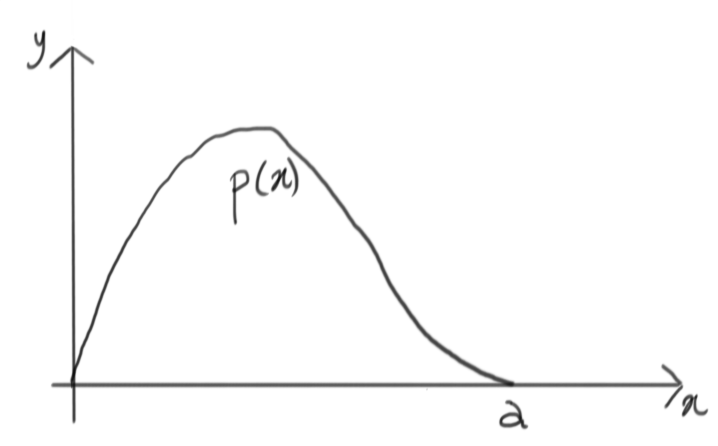
Let’s simplify, and encapsulate this complicated function within something simpler:

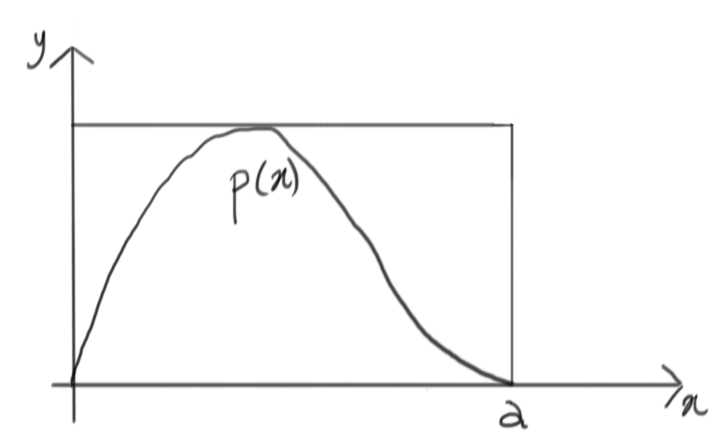
Of course this is not a probability density, but it’s easy to rescale it and get one, i.e. a uniform distribution between $0$ and $a$:

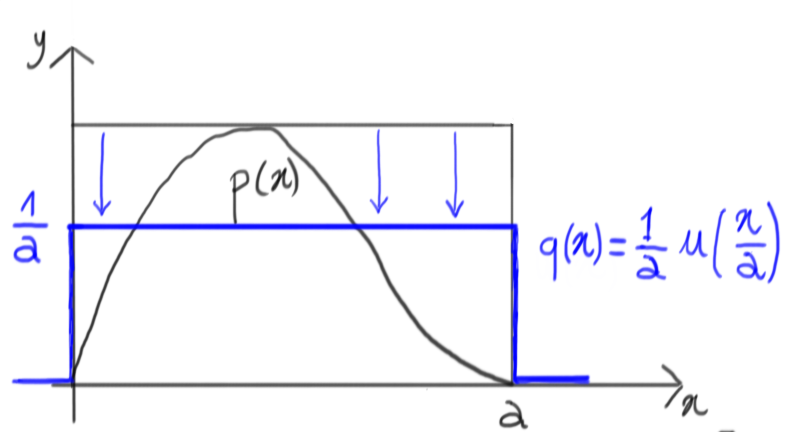
Let’s give it a try

Now, let’s generate a random number with this uniform density: as a matter of fact, we’re generating a number on the $x$ axis that is within the range where our original density $p(x)$ is non-zero:

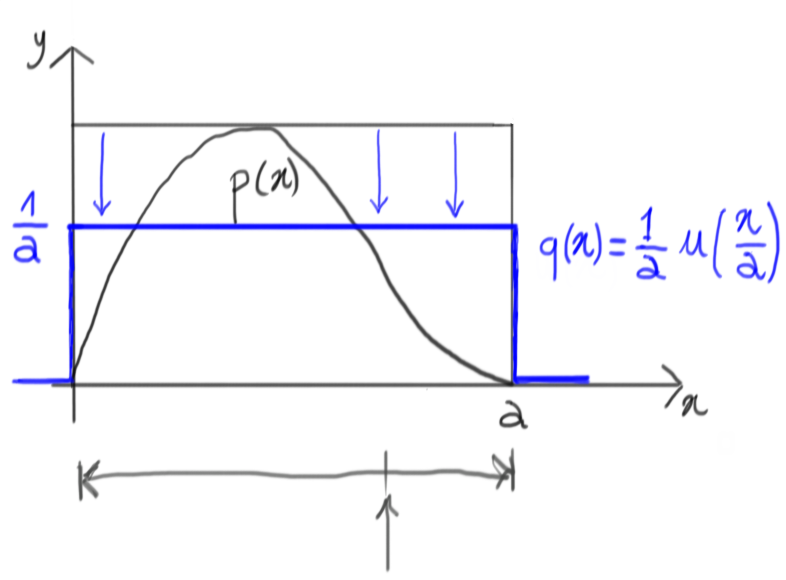
On the $y$ dimension, this lets us isolate a segment corresponding to that specific value of $x$ and extending from $0$ up to the total height of the containing rectangle:

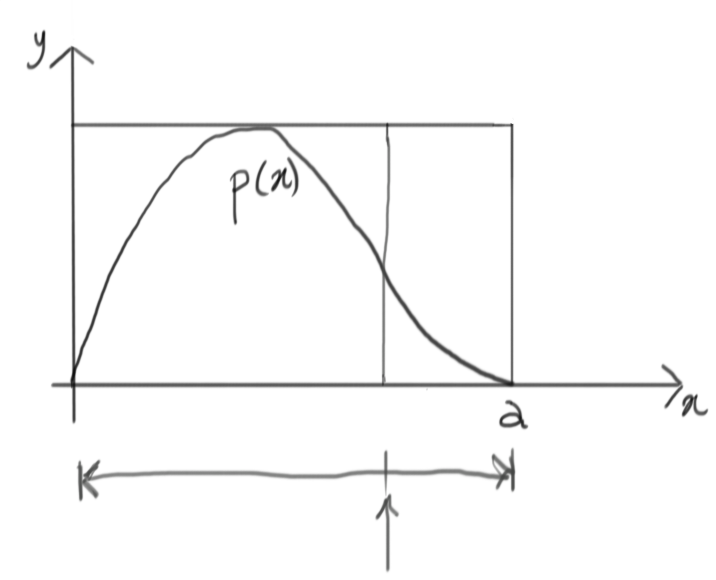
We can now generate another random number within this segment, again using a uniform distribution:

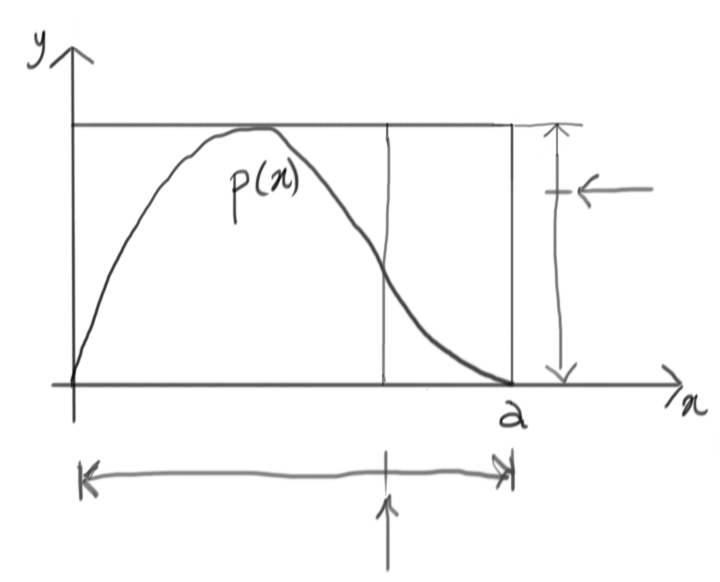
Now it’s time to accept this random draw or reject it. Whatever goes above the target $p(x)$ will be rejected, whatever goes under is accepted. In this case, we have a rejection.

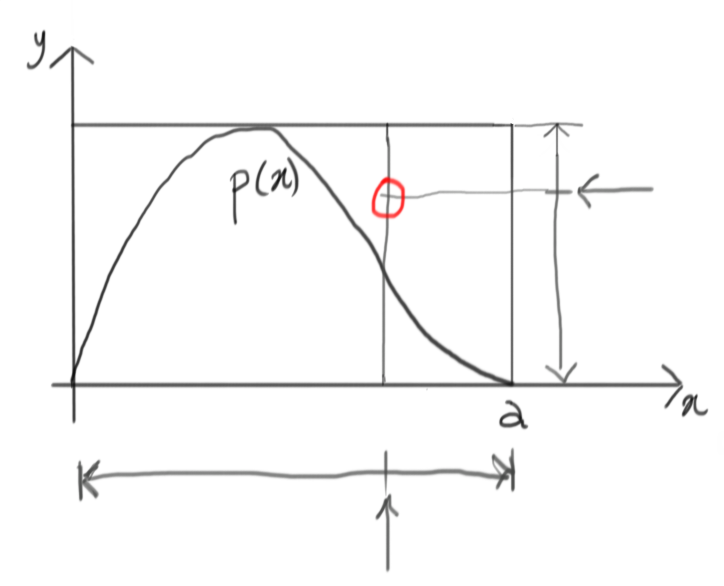
Time for a new try, then!

Let’s try again

Like before, we first generate a value on the $x$ dimension:

This gives us a new vertical segment:

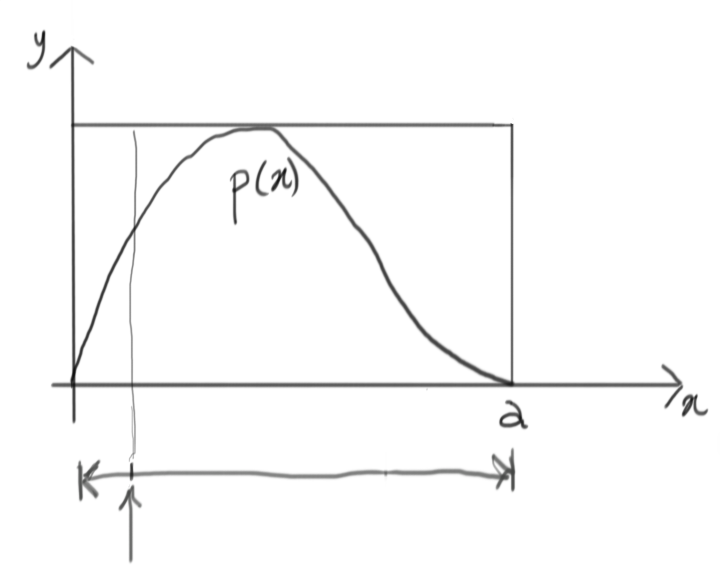
At this point, we can draw another uniform value in the vertical range:

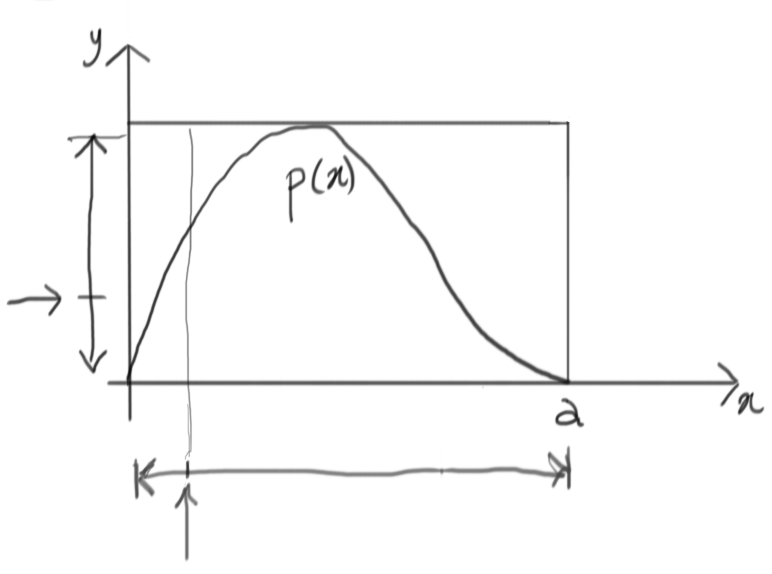
It seems that we were lucky this time: the value generated is below the corresponding value of $p(x)$ for the same $x$, so we accept this draw.

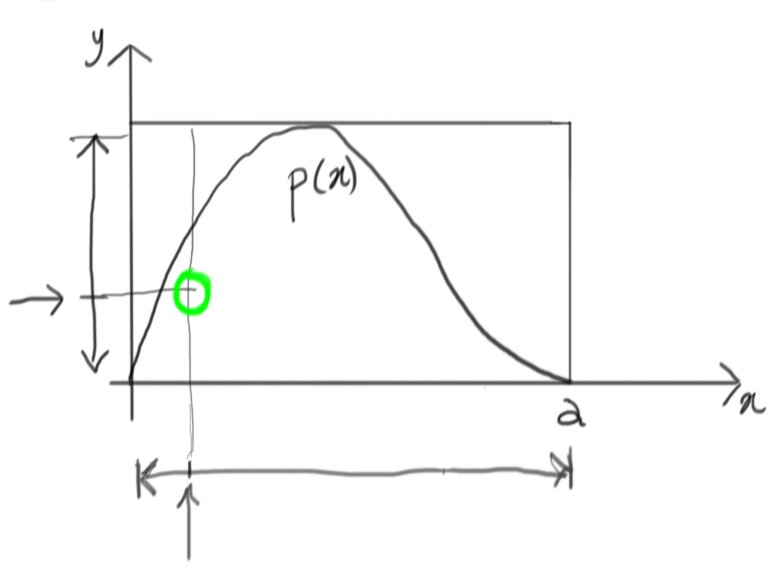
Will it work?

Without delving in a formal demonstration, it’s easy to see that this technique is going to work. Doing a lot of attempts, we end up with something like this:

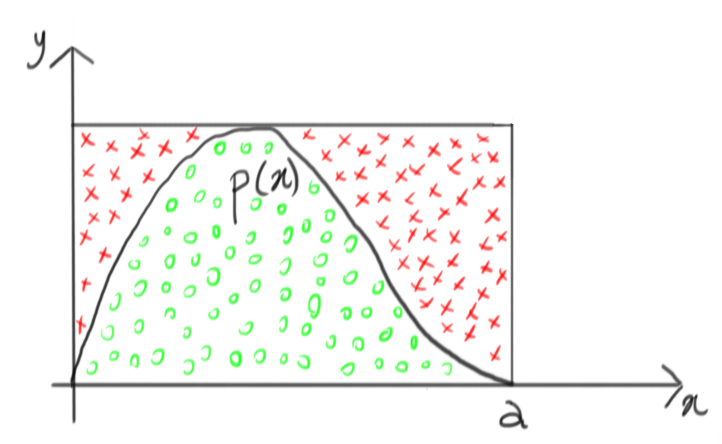
On the other hand, let’s remember that all the red crosses are rejected, so we can just as well ignore them and obtain this:

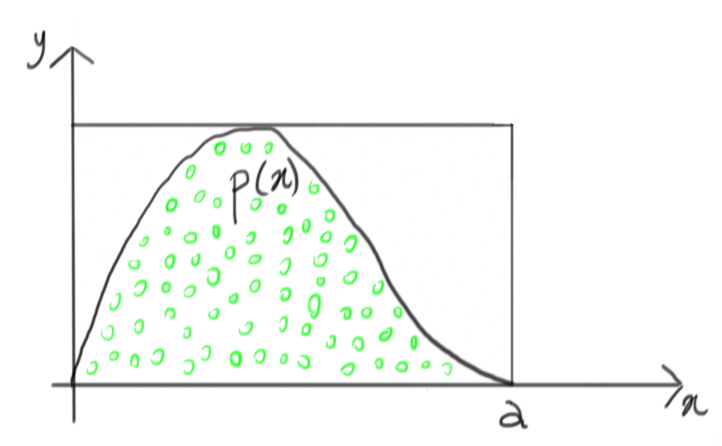
This, indeed, is very close to drawing samples from the target $p(x)$, isn’t it?