TL;DR

We add a search function to explore the solution space… and solve the puzzle.

After coding the constraints for our puzzle in Aquarium - constraints, we’re now ready to add a search function through all the possible candidates to fine one suitable for the constraints.

The complete code for this stage can be found in stage 4.

A search function

The search algorithm is coded directly into solve_puzzle, which so far only provided us hardcoded solutions. Here it is:

 1 sub solve_puzzle ($puzzle) {
 2    my $n = $puzzle->{n};
 3    $puzzle->{status} = [ map { [(0) x $n] } 1 .. $n ];
 4    my @stack;
 5    my $done;
 6    while (! $done) {
 7       try {
 8          apply_constraints($puzzle);
 9 
10          # if there are still unknown items, let's take a guess
11          $done = is_complete($puzzle);
12          if (! $done) {
13             my $guesser = moves_iterator($puzzle);
14             my $status = $guesser->(scalar @stack) # do first guess!
15                or die "no more guesses here\n";
16 
17             # save guesser for backtracking
18             push @stack, $guesser;
19 
20             # of course this is the new status
21             $puzzle->{status} = $status;
22          }
23       }
24       catch {
25          (my $e = $_) =~ s{\s+\z}{}gmxs;
26          while (@stack) { # backtrack until there's a new guess
27             if (my $status = $stack[-1]->(scalar @stack - 1)) {
28                $puzzle->{status} = $status;
29                last;
30             }
31             pop @stack;
32          }
33          die "unfeasible <$e>\n" unless @stack;
34       };
35    }
36    return $puzzle;
37 }

The field status inside $puzzle will track our solution. Every 1 represents a cell filled with water, a 0 represents an unknown cell and a -1 represents an empty cell. In this stage, though, we will only concentrate on filled cells, so we will just consider 1 and whatever is different from it. The status is initialized with all 0 values, meaning that we don’t know anything about it in the beginning.

We will have to search until we find a solution, so the while loop goes on until we are done (line 6). In each iteration:

• we check the constraints (line 8) inside a try block, because they may fail;
• if the constraints are OK, we will remain in the try block and see whether we are done or not (line 11). If there are still missing water cells (line 12), we will have to guess something (more on this later);
• if the constraints checks fail, an exception is thrown and we will end up in the catch block. Here we apply some backtracking (lines 26..32), if possible, or declare a defeat.

Checking if the puzzle is complete

After checking the constraints, we check whether we have a complete solution or not - i.e. if there are still cells that need to be assigned. This is where function is_complete helps us:

 1 sub is_complete ($puzzle) {
 2    my ($n, $items_by_row, $status) = $puzzle->@{qw< n items_by_row status >};
 3    my $missing = 0;
 4    for my $i (0 .. $n - 1) {
 5       $missing += $items_by_row->[$i];
 6       for my $j (0 .. $n - 1) {
 7          $missing-- if $status->[$i][$j] > 0;
 8       }
 9    }
10    return $missing == 0;
11 }

Assuming the puzzle is correct and only has one solution, it is sufficient to check whether the row-level constraints are matched exactly. To do this, we count how many missing water cells we have in each row, and return whether this number is zero (i.e. no missing cells) or not. Note that is_complete is called after the constraints validation, so we don’t risk having a false positive.

Guessing moves

When constraints are OK, but we still have missing water cells, we have to take guesses. We encapsulate this moves-guessing in an iterator function that checks all possible guesses for a given starting position. Function moves_iterator generates an iterator that gives out these guesses.

 1 sub moves_iterator ($puzzle) {
 2    my ($n, $field) = $puzzle->@{qw< n field >};
 3    my $original_status = dclone($puzzle->{status});
 4    my $i = $n - 1;
 5    my $j = 0;
 6    my %done;
 7    return sub {
 8       my $status = dclone($original_status);
 9       while ($i >= 0) {
10          while ($j < $n) {
11             next if $status->[$i][$j]; # look for unknown spots
12             my $id = $field->[$i][$j];
13             next if $done{$id}++;
14             for my $tmp_j ($j .. $n - 1) {
15                next unless $field->[$i][$tmp_j] == $id;
16                $status->[$i][$tmp_j] = 1; # try water here
17             }
18             return $status;
19          }
20          continue {
21             $j++;
22          }
23       }
24       continue {
25          $i--;
26          $j = 0;
28       }
29       return;
30    };
31 }

It is basically the implementation of a nested loop that is interrupted each time a guess is available. The original status is saved at the beginning (line 3) and used over and over to generate guesses (line 16 and line 18).

The search is performed from bottom to top, because water falls down and it’s easier to find a solution in this way.

For each line, we keep track of the identifiers that we try out, and avoid re-scanning them afterwards (line 13).

Backtracking

When a specific configuration is rejected by the constraints, an exception is thrown and backtracking kicks in.

 1 sub solve_puzzle ($puzzle) {
...
24       catch {
25          (my $e = $_) =~ s{\s+\z}{}gmxs; 26          while (@stack) { #
26          while (@stack) { # backtrack until there's a new guess
27             if (my $status = $stack[-1]->(scalar @stack - 1)) {
28                $puzzle->{status} = $status;
29                last;
30             }
31             pop @stack;
32          }
33          die "unfeasible <$e>\n" unless @stack;
34       };
35    }
36    return $puzzle;
37 }

This basically consists in calling the move-guessing function over and over (line 27), until a new candidate is available (i.e. $status is defined) or the possibilities are exhausted in the specific frame of the stack and we have to backtrack further (line 31). If the puzzle has a solution we will eventually get to the end of it, otherwise… we will die (line 33).

Constraints application

All constraints checking is encapsulated in apply_constraints:

 1 sub apply_constraints ($puzzle) {
 2    assert_water_level($puzzle);
 3    assert_boundary_conditions($puzzle);
 4 }

This calls our functions for checking constrints… for the moment. It might change in the future 🙄

Let’s check it!

Well, time to run our solver then:

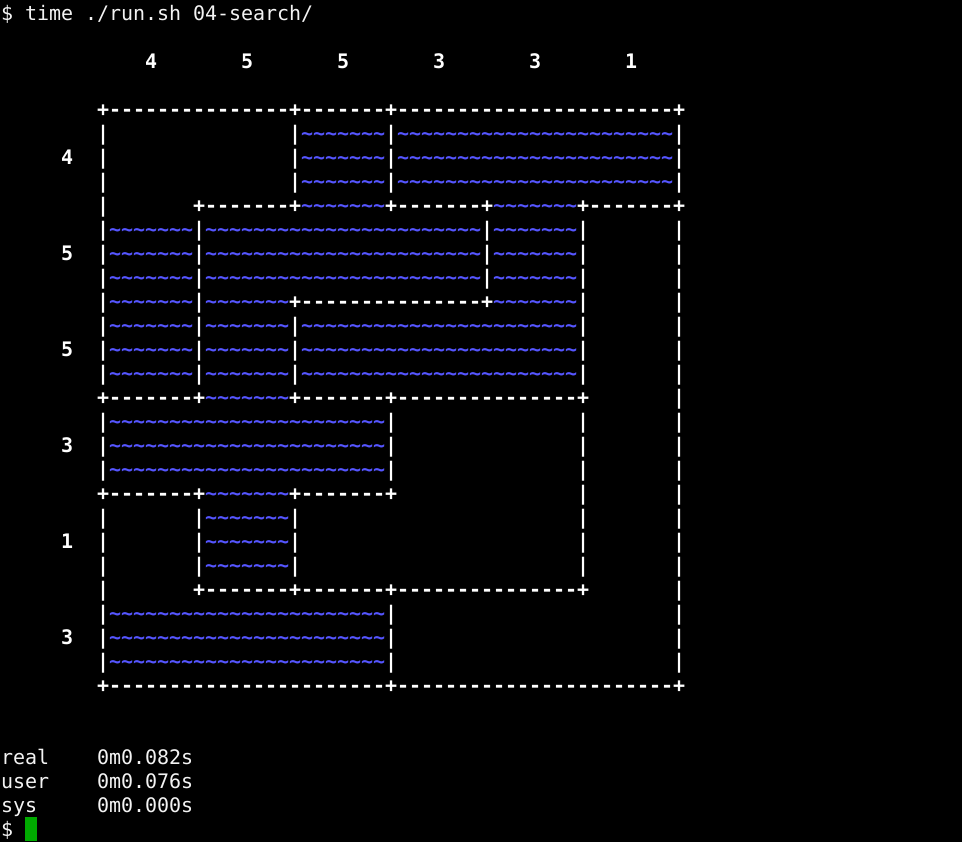
It works! And it seems to run in an adequate amount of time.

Or does it?

Alas, our solver is very, very far from perfection - or useability. Let’s see how it goes with a slightly more difficult puzzle, one with 6 cells border and normal difficulty:

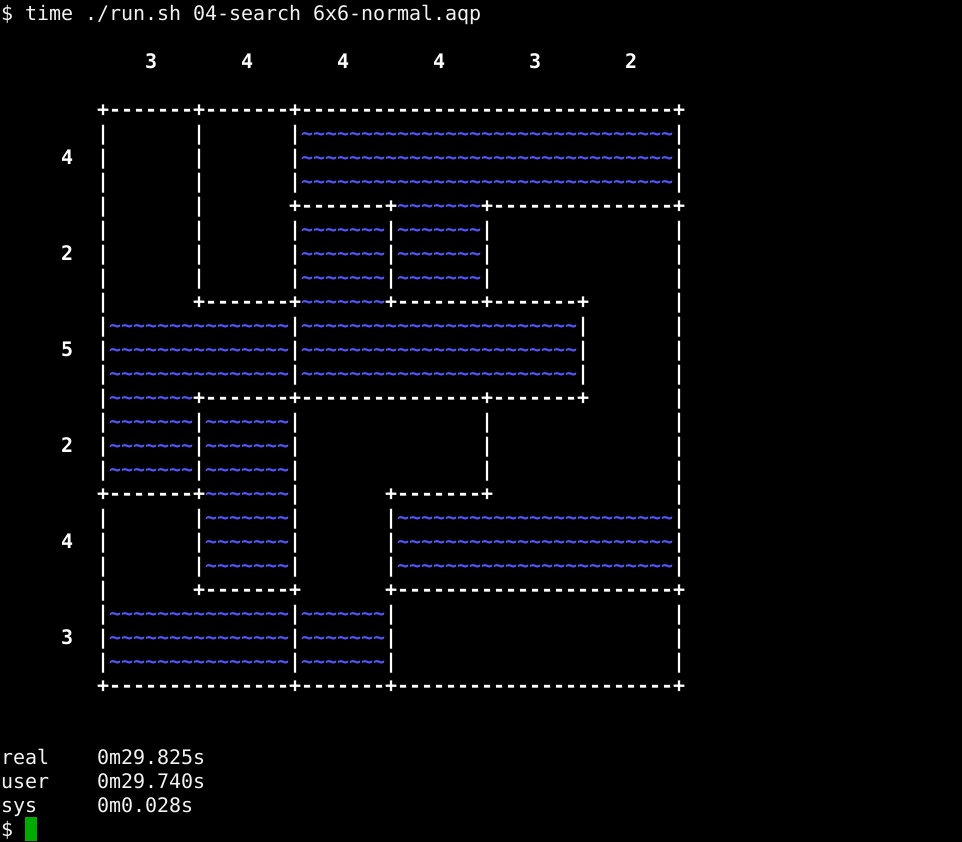
We jumped up to 30 seconds in a breeze. The increase in difficulty is mostly related to the number of aquariums: the easy example has 6, the normal one has 9. I just stopped running examples for 6x6 hard (18 aquariums) and 10x10 normal (13 aquariums).

This is easily understood: our algorithm does very feeble attempts at pruning the search space - it cuts out sub-trees that cannot exist, but it does nothing at cutting out impossible situations before testing them.

There’s definitely space for improvement.