TL;DR

Making only one constraint cooperate is a good start, but we can do better. And we will!

The code for this post can be found in stage 6.

Getting the most out of row and column constraints

Let’s take a look at the following row in a possible puzzle:

        +---------------+-------+-----------------------+
        |               |       |                       |
     4  |               |       |                       |
        |               |       |                       |
        |       +-------+~~~~~~~+-------+       +-------+

Can we infer anything from it? Yes, definitely!

Let’s first observe that the three-cells block on the right can either be completely empty, or completely full. There’s no half-way, because the rules of the game tell us so.

At this point we can ask ourselves: can it be empty? Certainly not! If we miss this precious three-cells spot, we will be left with only 3 candidate cells on this row for holding water, which is never going to address the need to have 4 spots filled with water. As a consequence… it must be filled with water:

        +---------------+-------+-----------------------+
        |               |       |~~~~~~~~~~~~~~~~~~~~~~~|
     4  |               |       |~~~~~~~~~~~~~~~~~~~~~~~|
        |               |       |~~~~~~~~~~~~~~~~~~~~~~~|
        |       +-------+~~~~~~~+-------+~~~~~~~+-------+

Now we can also do a similar reasoning about the two-cells spot on the left, which - again - it’s take-all or leave-all. Can it possibly be part of the solution? Surely not! If we include it, we end up with 5 filled cells in this row, which is not allowed. Hence, we must set this spot to empty:

        +---------------+-------+-----------------------+
        |               |       |~~~~~~~~~~~~~~~~~~~~~~~|
     4  |   X       X   |       |~~~~~~~~~~~~~~~~~~~~~~~|
        |               |       |~~~~~~~~~~~~~~~~~~~~~~~|
        |       +-------+~~~~~~~+-------+~~~~~~~+-------+

Now, of course, there’s only one way to fulfil the constraint, i.e. put water in the remaining unknown cell:

        +---------------+-------+-----------------------+
        |               |~~~~~~~|~~~~~~~~~~~~~~~~~~~~~~~|
     4  |   X       X   |~~~~~~~|~~~~~~~~~~~~~~~~~~~~~~~|
        |               |~~~~~~~|~~~~~~~~~~~~~~~~~~~~~~~|
        |       +-------+~~~~~~~+-------+~~~~~~~+-------+

This was an easy line, because we were able to figure it out completely by itself. Life is not always this easy, but this trick is surely interesting to consider and get some pruning from our extensive search.

There is also a similar - although less powerful - version of this constraint that can be applied to column-wise constraints. Can you figure it out?

Let’s code this

The following function turn the insights of the previous section into code:

 1 sub adjust_by_row ($puzzle) {
 2    my ($n, $items_by_row, $field, $status)
 3       = $puzzle->@{qw< n items_by_row field status >};
 4    my $acted = 0;
 5    for my $i (0 .. $n - 1) {
 6       my $needed = $items_by_row->[$i];
 7       my $available = $n;
 8       my %available_by_id;
 9       for my $j (0 .. $n - 1) {
10          $needed-- if $status->[$i][$j] > 0;
11          $available-- if $status->[$i][$j];
12          my $id = $field->[$i][$j];
13          push $available_by_id{$id}->@*, $j unless $status->[$i][$j];
14       }
15       die 'unfeasible' if $needed < 0;
16       die 'unfeasible' if $needed > $available;
17       for my $id (keys %available_by_id) {
18          my $av = $available_by_id{$id};
19          if ($av->@* > $needed) { # can't serve this here
20             $status->[$i][$_] = -1 for $av->@*;
21             $acted++;
22          }
23          elsif ($available - $av->@* < $needed) { # need this
24             $status->[$i][$_] = 1 for $av->@*;
25             $acted++;
26          }
27       }
28    }
29    return $acted;
30 }

Rows are analyzed from top to bottom (line 5). It would also work in reverse, because this constraint is only focused on one row at a time.

There are two sweeps:

• the first sweep (lines 9..14) analyze the row and get some data: how many unknown spots (named available) are there, both in total and by aquarium id, as well as how many of them still need to be allocated some water (variable $needed).
• the second sweep implements the insight of the previous section, both inclusively and exclusively:
  • lines 19..22 check whether a specific aquarium would overflow the need, excluding it if this is the case (just like the example of the two-cells spot in the previous section);
  • lines 23..26 check whether excluding a specific aquarium would result in an excessive loss of available spots, and forces its inclusion if it does (just liek the example of the three-cells spot in the previous section).

Between the two sweeps there is a sanity check: if the number of needed cells dropped below 0, it means that we filled too many cells; otherwise, if it’s beyond the number of available unknown spots, we are never going to fulfil this constraint. In both cases we throw an exception.

Let’s code the column-wise pruning constraint too

As anticipated, there is a weaker version of the deduction-by-constraint trick that can be applied to columns, here is the code for it:

 1 sub adjust_by_col ($puzzle) {
 2    my ($n, $items_by_col, $field, $status)
 3       = $puzzle->@{qw< n items_by_col field status >};
 4    my $acted = 0;
 5    for my $j (0 .. $n - 1) {
 6       my $needed = $items_by_col->[$j];
 7       my $available = $n;
 8       my %available_by_id;
 9       for my $i (0 .. $n - 1) {
10          $needed-- if $status->[$i][$j] > 0;
11          $available-- if $status->[$i][$j];
12          my $id = $field->[$i][$j];
13          push $available_by_id{$id}->@*, $i unless $status->[$i][$j];
14       }
15       die 'unfeasible' if $needed < 0;
16       die 'unfeasible' if $needed > $available;
17       for my $id (keys %available_by_id) {
18          my $av = $available_by_id{$id};
19          if ($available - $av->@* < $needed) { # need this
20             my $take = $needed - ($available - $av->@*);
21             $status->[pop $av->@*][$j] = 1 for 1 .. $take;
22             $available -= $take;
23             $needed -= $take;
24             $acted++;
25          }
26          elsif ($av->@* > $needed) { # remove excess
27             $status->[shift $av->@*][$j] = -1 while $av->@* > $needed;
28             $acted++;
29          }
30          # there should be more to this
31       }
32    }
33    return $acted;
34 }

As before, we have an outer loop sweeping through columns, then two sequential inner loops sweeping through rows. The first of these two inner loops collects data, the second makes the inferences and updates the status if possible. Again, there is a sanity check in between.

Let’s put these new constraints at work

The two new constraints together are an enhanced version of the previous constraint about row and column values, so we can remove the old one and put thest two instead:

sub apply_constraints ($puzzle) {
   my $changes = -1;
   while ($changes != 0) {
      $changes = 0;
      $changes += adjust_water_level($puzzle);
      $changes += adjust_by_col($puzzle);
      $changes += adjust_by_row($puzzle);
   }
}

How does it go?

Things are getting definitely better with this enhancement, the 6x6 are now all tackled, the 10x10 are fine up to level normal and we might get a 10x10 hard puzzle solved in a reasonable time if we get particularly lucky.

This is an example for a 10x10 normal:

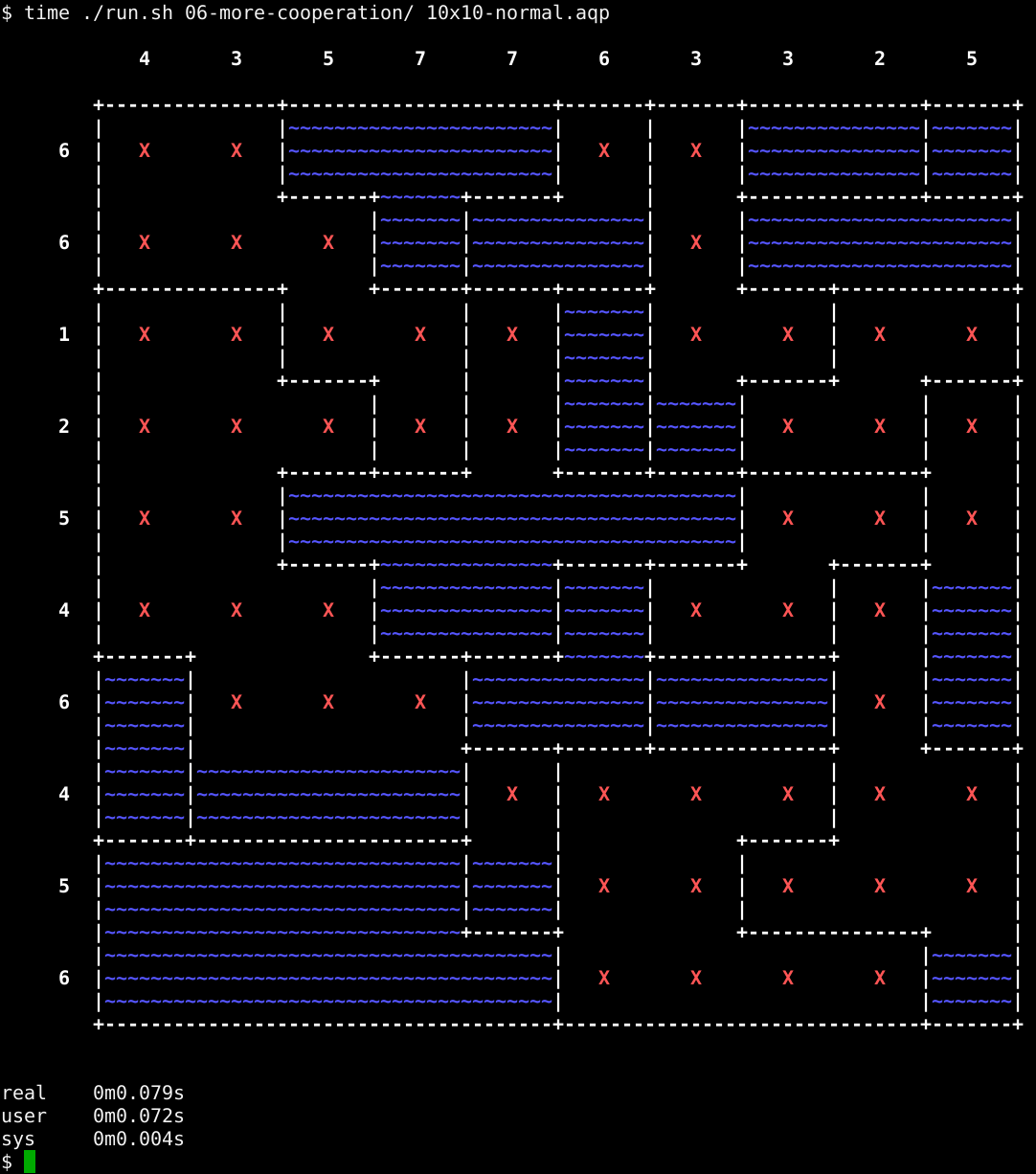
But let’s not start suc*AHEM* get too excited yet: most of the 10x10 hard problems are still too slow, and we have to address the 15x15, the daily, the weekly and the monthly puzzles yet!