ETOOBUSY 🚀 minimal blogging for the impatient
PWC145 - Palindromic Tree
TL;DR
On with TASK #2 from The Weekly Challenge #145. Enjoy!
The challenge
You are given a string
$s.Write a script to create a
Palindromic Treefor the given string.I found this blog exaplaining
Palindromic Treein detail.Example 1:
Input: $s = 'redivider' Output: r redivider e edivide d divid i ivi vExample 2:
Input: $s = 'deific' Output: d e i ifi f cExample 3:
Input: $s = 'rotors' Output: r rotor o oto t sExample 4:
Input: $s = 'challenge' Output: c h a l ll e n gExample 5:
Input: $s = 'champion' Output: c h a m p i o nExample 6:
Input: $s = 'christmas' Output: c h r i s t m a
The questions
At the end of the day the data structure and the algorithm to create it come out clear, although the blog post seems to have a few spaces for enhancement. The original paper seems to make a point to be very, very blunt.
Sometimes I think the academic world seems so eager to publish, and yet so reluctant to share.
What’s my question? None actually, just took the chance to rant a bit.
The solution
Both Perl and Raku allow to write perfectly readable code. I would even go to the point of calling it amazingly readable code, but I might be biased. So, instead of explaining the algorithm once again, I’ll just start laying it down, Perl first:
sub new ($package, $string) {
my @suffixes = (
{ length => -1, pred => 0 },
{start => 0, length => 0, pred => 0 },
);
for my $i (0 .. length($string) - 1) {
my $c = substr $string, $i, 1;
# find longest suffix Q such that cQc exists
my $Q = $suffixes[-1];
while ($Q->{length} >= 0) {
my $j = $i - $Q->{length} - 1; # "mirror" of $i
last if $j >= 0 && $c eq substr $string, $j, 1;
$Q = $suffixes[$Q->{pred}];
}
next if exists $Q->{expansion_for}{$c};
# adding a node as an expansion from $Q
push @suffixes, {
start => $i - $Q->{length} - 1,
length => $Q->{length} + 2,
pred => 1, # this is just an educated guess default
};
$Q->{expansion_for}{$c} = $#suffixes;
next if $Q->{length} < 0; # solitary, no further search needed
$Q = $suffixes[$Q->{pred}]; # start from the previous one
while ($Q->{length} >= 0) {
my $j = $i - $Q->{length} - 1; # "mirror" of $i
last if $j >= 0 && $c eq substr $string, $j, 1;
$Q = $suffixes[$Q->{pred}];
}
$suffixes[-1]{pred} = $Q->{expansion_for}{$c};
}
return bless {
string => $string,
suffixes => \@suffixes,
}, $package;
}
This is, of course, part of a larger program.
The algorithm is about building up a graph with nodes and edges. In our case:
- nodes are represented by (anonymous) hashes, containing details
about the substring they represent (in terms of a
startandlength, referred to the input string) - edges are put inside the nodes, in particular:
- key
predpoints to the smaller prefix up in the graph; - key
expansions-forpoints to a hash where keys are single characterscand values are indexes for nodescQc.
- key
All nodes are stored in an array @sequences and managed through their
index inside the array itself.
A couple observations:
- the algorithm is an online algorithm, i.e. it is capable of dealing with characters addition on the right, one at a time. The complexity is actually evaluated for the addition of a single character, as I get it, so the building of the whole graph takes $O(N^2)$ (with $N$ length of the string and a fixed dictionary size).
- due to this, we’re always focusing on the last part of the substring that is immediately precedent the character we have to add. This makes sense because we have to figure out if and how the new character fits in adding some palindromic stuff in our data structure. This is why we’re always reading about suffix-something.
A new node is added only if it’s not already present. When we have to add it, the structure is mostly the same all the times, where the only thing that might change between those whose length is 1 and the other ones is the precedent node (for lengths equal to 1 it’s always the empty string).
As you can see, the algorithm to find the precedent is exactly the same as the one to find the right maximal-length suffix.
Well… Raku time, with an almost 1-1 translation:
method new ($string) {
my @suffixes =
hash( 'length', -1, 'pred', 0),
hash('start', 0, 'length', 0, 'pred', 0);
for 0 ..^ $string.chars -> $i {
my $c := $string.substr: $i, 1;
# find longest suffix Q such that cQc exists
my $Q = @suffixes[*-1];
while ($Q<length> >= 0) {
my $j = $i - $Q<length> - 1; # "mirror" of $i
last if $j >= 0 && $c eq $string.substr($j, 1);
$Q = @suffixes[$Q<pred>];
}
next if $Q<expansion-for>{$c}:exists;
# adding a node as an expansion from $Q
@suffixes.push: hash(
'start', $i - $Q<length> - 1,
'length', $Q<length> + 2,
'pred', 1, # this is just an educated guess default
);
$Q<expansion-for>{$c} = @suffixes.end;
next if $Q<length> < 0; # solitary, no further search needed
$Q = @suffixes[$Q<pred>]; # start from the previous one
while ($Q<length> >= 0) {
my $j = $i - $Q<length> - 1; # "mirror" of $i
last if $j >= 0 && $c eq $string.substr($j, 1);
$Q = @suffixes[$Q<pred>];
}
@suffixes[*-1]<pred> = $Q<expansion-for>{$c};
}
self.bless(:$string, :@suffixes);
}
Again, there’s a full version of the Raku program.
One thing I tripped over is the initialization of the hash for new
nodes, which was initially written like this:
@suffixes.push: hash(
start => $i - $Q<length> - 1,
length => $Q<length> + 2,
pred => 1, # this is just an educated guess default
);
Alas, this initializes the hash with pairs, whose values are immutable:
Cannot assign to an immutable value
So… I miss the fat comma a bit!
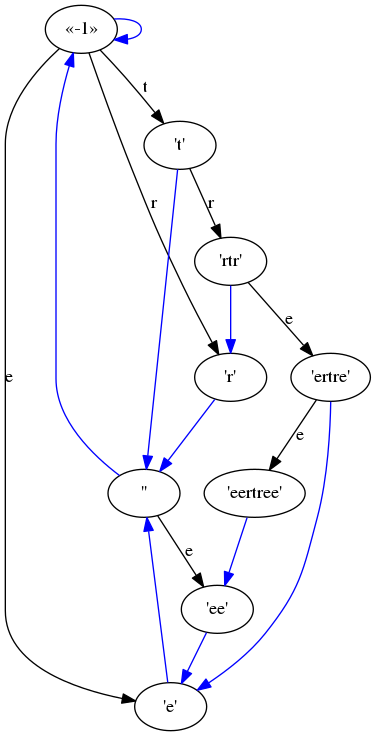
Both programs implement a dot method that outputs something like this:
digraph {
"«-1»" -> "«-1»" [color=blue]
"«-1»" -> "'r'" [color=black label="r"]
"«-1»" -> "'e'" [color=black label="e"]
"«-1»" -> "'t'" [color=black label="t"]
"''" -> "«-1»" [color=blue]
"''" -> "'ee'" [color=black label="e"]
"'e'" -> "''" [color=blue]
"'ee'" -> "'e'" [color=blue]
"'r'" -> "''" [color=blue]
"'t'" -> "''" [color=blue]
"'t'" -> "'rtr'" [color=black label="r"]
"'rtr'" -> "'r'" [color=blue]
"'rtr'" -> "'ertre'" [color=black label="e"]
"'ertre'" -> "'e'" [color=blue]
"'ertre'" -> "'eertree'" [color=black label="e"]
"'eertree'" -> "'ee'" [color=blue]
}
This can be fed to Graphviz’s dot to obtains something like this:
This was the last post on The Weekly Challenge for 2021… stay safe everybody and have a good end of the year, as well as a fantastic start of the new one!