TL;DR

Additional notes on the orthogonality of two vectors.

In previous post PWC123 - Square Points there is this statement, which might appear as having been drawn out of thin air:

Checking for orthogonality can be done calculating their regular scalar (or dot) product:

\[v \cdot w = v_x w_x + v_y w_y\]

This is 0 if and only if the two vectors are orthogonal, so it’s exactly the condition we are after.

So we have two vectors $\vec{v} = (v_1, …, v_n)$ and $\vec{w} = (w_1, …, w_n)$ (where $n = 2$ in the case of the previous post, but we’re aiming for the big, general case here) and we want to understand whether they’re orthogonal or not, based on their scalar product. Let’s go!

If they are, then $\vec{v}$ is also orthogonal to $-\vec{w}$, because $\vec{w}$ and $-\vec{w}$ are 180° apart from each other.

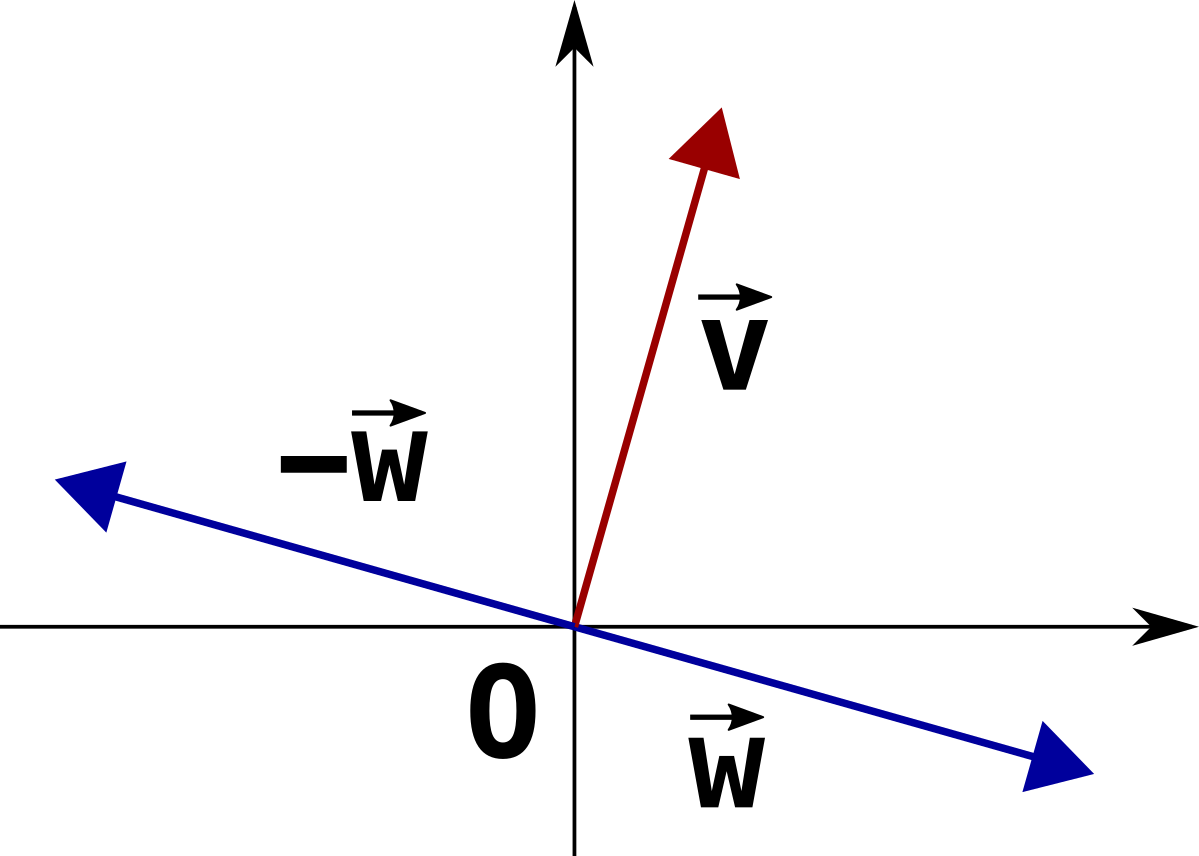
Let’s now consider a triangle $\overset{\triangle}{ABC}$ where:

\[A = O + \vec{w} \\ B = O - \vec{w} \\ C = O + \vec{v}\]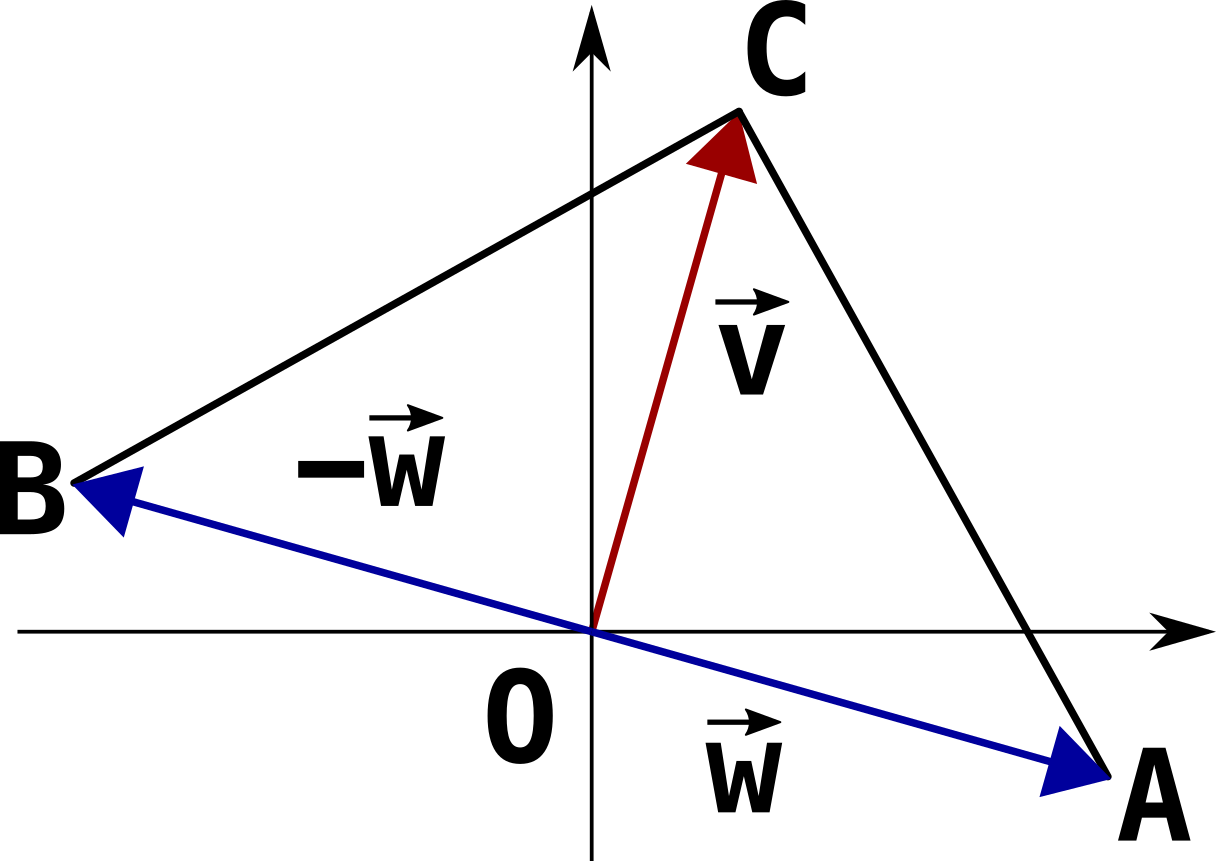

Sub-triangles $\overset{\triangle}{AOC}$ and $\overset{\triangle}{BOC}$ are congruent, which practically speaking means that they’re the same triangle with some translation and/or rotation and/or flipping (but no scaling). They satisfy the so-called Side-Angle-Side (SAS) condition for congruence, because:

• $\overline{OA}$ and $\overline{OB}$ have the same length:

\[L_{\overline{OA}} = |\vec{w}| = |-\vec{w}| = L_{\overline{OB}}\]

• $\overline{OC}$ is in common;

• angles in between $\widehat{AOC}$ and $\widehat{BOC}$ are both 90°.

This implies that segments $\overline{AC}$ and $\overline{BC}$ have the same length so, by extension, the square of their lengths:

\[L_{\overline{AC}}^2 = |\vec{v} - \vec{w}|^2 = \sum_{i=1}^{n}(v_i - w_i)^2 = \sum_{i=1}^{n}(v_i^2 - 2 v_i w_i + w_i^2) \\ L_{\overline{BC}}^2 = |\vec{v} - (-\vec{w})|^2 = \sum_{i=1}^{n}(v_i + w_i)^2 = \sum_{i=1}^{n}(v_i^2 + 2 v_i w_i + w_i^2)\]

are the same, i.e. their difference is $0$:

\[L_{\overline{BC}}^2 - L_{\overline{AC}}^2 = 0 \\ \sum_{i=1}^{n}(v_i^2 + 2v_i w_i + w_i^2 - v_i^2 + 2v_i w_i - w_i^2) = 0 \\ 4 \sum_{i=1}^{n}v_i w_i = 0 \\ \sum_{i=1}^{n}v_i w_i = 0 \iff \vec{v} \cdot \vec{w} = 0\]

i.e. the scalar product (a.k.a. dot product) between $\vec{v}$ and $\vec{w}$ is $0$.

On the other hand, it’s easy to go in the opposite direction: if the scalar product is $0$, then either one of the two vectors is the null vector (which is assumed to be orthogonal to any other vector, by definition), or they must form a triangle that satisfy the relation above where the length of $\overline{AC}$ is the same as the length of $\overline{BC}$, which in turn implies that segment $\overline{OC}$ is the height of the isosceles triangle and that angle $\widehat{AOC}$ is 90°.

Summing up, then:

\[\vec{v} \perp \vec{w} \iff \vec{v} \cdot \vec{w} = 0\]

which is the property we used in the previous post. What a ride, whew!

I find this fact awesome: by just doing some very simple arithmetics over the coordinates of the vectors we can easily establish if they’re perpendicular as geometric objects.

Enough for today… stay safe folks!