ETOOBUSY 🚀 minimal blogging for the impatient
Area of a triangle
TL;DR
I was thinking about calculating the area of a triangle…
… for reasons that go beyond this post, and I obviously started from the basic formula we were all teached in school: base times height divided by two. So with reference to the following picture:
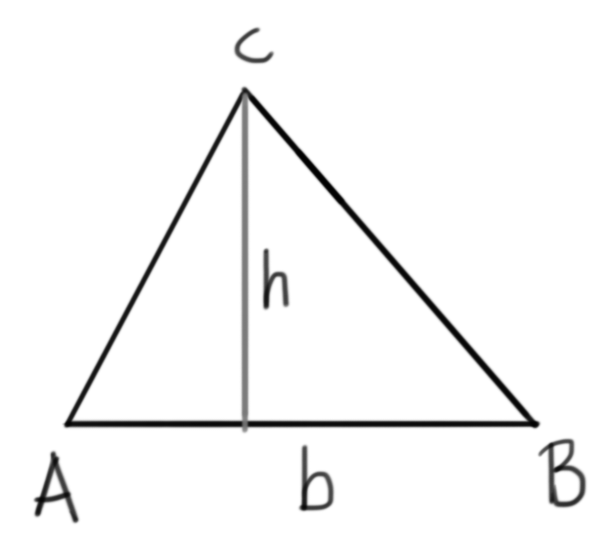
we have that segment $\overline{AB}$ is the base $b$ and the height with respect to it is h. In this case, then, we have that area $S$ is:
\[S = \frac{b \cdot h}{2}\]Easy, right? Now let’s assume that you are given a triangle by its coordinates in the cartesian plane $XY$:
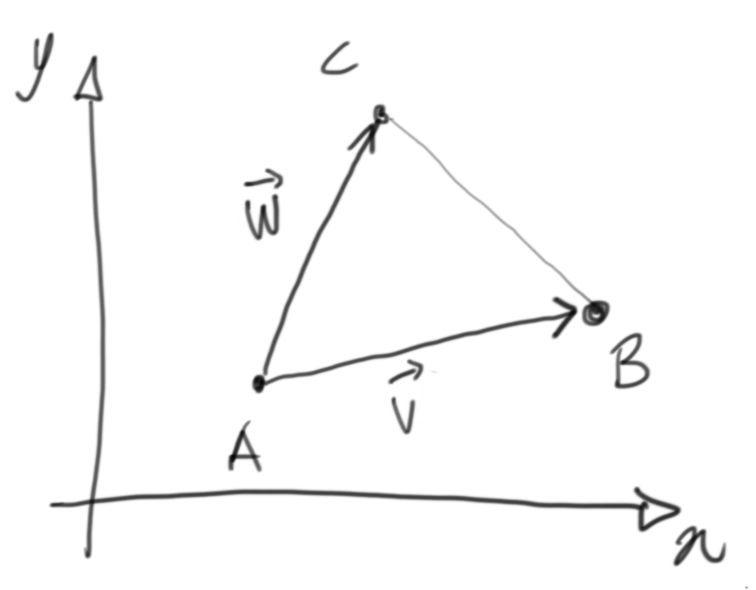
In this case, we are given the three points:
\[\mathbf{A} = (A_x, A_y) \\ \mathbf{B} = (B_x, B_y) \\ \mathbf{C} = (C_x, C_y)\]How to calculate the area in this case? Well…
First of all, let’s switch to vectors
It’s easy to see that vectors $\vec{v}$ and $\vec{w}$ actually are an arrowized version of the two sides $\overline{AB}$ and $\overline{AC}$ respectively. This means that wherever we place these two vectors applied to a point in the plane, it will be the same triangle moved around and the area will be the same.
Long story short… we will work with these two vectors:
\[\vec{v} = (v_x, v_y) = (B_x - A_x, B_y - A_y) \\ \vec{w} = (w_x, w_y) = (C_x - A_x, C_y - A_y)\]How to calculate the area, then?
Let’s just get back to the origins…
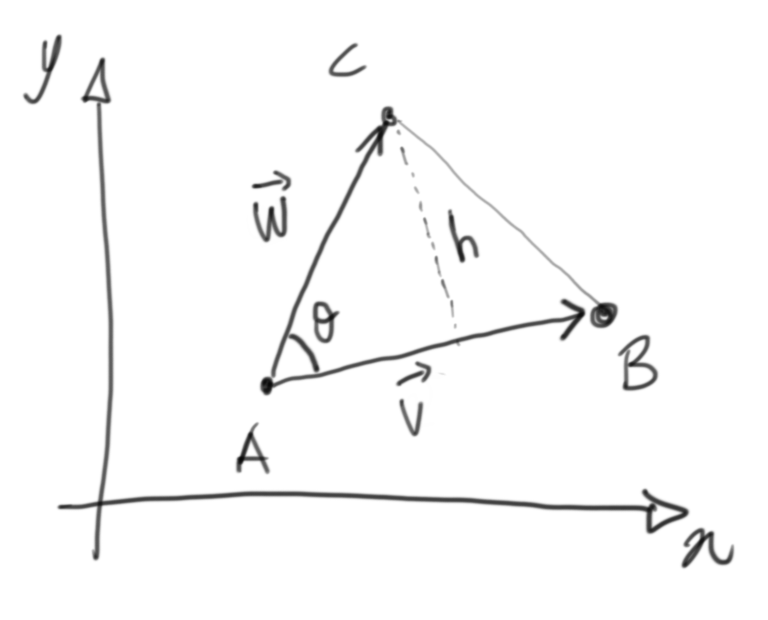
The base $b$ is just the length of vector $\vec{v}$, which we will represent like this:
\[b = |v| = \sqrt{v_x^2 + v_y^2}\]Now the corresponding height $h$ can be calculated like this:
\[h = |w| \cdot sin\theta = \sqrt{w_x^2 + w_y^2} \cdot sin\theta\]So… the area $S$ will be:
\[S = \frac{b \cdot h}{2} = \frac{|v|\cdot |w| \cdot sin\theta}{2}\]So what’s with this angle?!?
It turns out that you can calculate the scalar product of the two vectors in a pretty straightforward way, and it is indeed related to the cosine of the angle $\theta$:
\[\vec{v}\cdot\vec{w} = v_x \cdot w_x + v_y \cdot w_y = |v| \cdot |w| \cdot cos\theta\]which means:
\[cos\theta = \frac{\vec{v}\cdot\vec{w}}{|v| \cdot |w|}\]Now we just have to remember Pythagora’s theorem:
\[sin^2\theta + cos^2\theta = 1 \\ sin^2\theta = 1 - cos^2\theta \\ sin^2\theta = 1 - \frac{(\vec{v}\cdot\vec{w})^2}{|v|^2 \cdot |w|^2} \\ sin^2\theta = \frac{|v|^2 \cdot |w|^2 - (\vec{v}\cdot\vec{w})^2}{|v|^2 \cdot |w|^2}\]We will concentrate on the positive value for the sine (so that we get positive areas), so:
\[sin\theta = \frac{\sqrt{|v|^2 \cdot |w|^2 - (\vec{v}\cdot\vec{w})^2}}{|v| \cdot |w|}\]Let’s multiply by the denominator on both sides… and divide by two as well:
\[\frac{|v| \cdot |w| \cdot sin\theta}{2} = \frac{\sqrt{|v|^2 \cdot |w|^2 - (\vec{v}\cdot\vec{w})^2}}{2}\]Now wait! The left hand side is our area $S$, so…
\[S = \frac{\sqrt{|v|^2 \cdot |w|^2 - (\vec{v}\cdot\vec{w})^2}}{2} \\ S = \frac{\sqrt{(v_x^2 + v_y^2) \cdot (w_x^2 + w_y^2) - (v_x \cdot w_x + v_y \cdot w_y)^2}}{2}\]Did you notice?
The scalar(dot) product of a generic vector $\vec{v}$ with itself ends up being the square of its length:
\[\vec{v}\cdot\vec{v} = |v|^2\]so our area can also be expressed as:
\[S = \frac{ \sqrt{ (\vec{v}\cdot\vec{v})\cdot(\vec{w}\cdot\vec{w}) - (\vec{v}\cdot\vec{w})\cdot(\vec{v}\cdot\vec{w}) } }{2}\]Nifty, uh?!?
It’s easier with some code
After this long ride, let’s just take a look at some code. We assume
that our points are represented by arrays (references) with $X$
coordinate at index 0 and $Y$ coordinate at index 1;
sub triangle_area {
my ($A, $B, $C) = @_;
my ($v_x, $v_y) = map {$B->[$_] - $A->[$_]} 0 .. 1;
my ($w_x, $w_y) = map {$C->[$_] - $A->[$_]} 0 .. 1;
my $vv = $v_x * $v_x + $v_y * $v_y;
my $ww = $w_x * $w_x + $w_y * $w_y;
my $vw = $v_x * $w_x + $v_y * $w_y;
return sqrt($vv * $ww - $vw * $vw) / 2;
}
And I guess we’re done for today!